Skip to content

Evolutionary Algorithms: Introduction


Evolutionary Algorithms (EAs) are a subset of optimization algorithms inspired by the process of natural selection and genetics. Imagine a population of "candidate solutions" evolving over generations, with the fittest solutions surviving and reproducing, passing on their traits.

Business Optimization with EA

Evolutionary Algorithms shine in business because many real-world problems aren't simple linear equations. They involve complex trade-offs, countless variables, and emergent behaviors. EAs provide a way to navigate this complexity and find high-performing, often non-obvious, solutions.

💼 Project Selection & Budgeting

A company has a fixed annual budget of $5 million and a list of 50 potential projects. Each project has an estimated cost and an expected return on investment (ROI). Which combination of projects should be funded to maximize the total ROI without exceeding the budget?

With 50 projects, there are 2502^{50} (over a quadrillion) possible combinations. It's impossible to check them all.

🗺️ Facility Location

A retail chain wants to open 5 new distribution centers to serve 100 store locations. Given a list of 30 potential sites for the new centers, which 5 sites should be chosen to minimize the total shipping distance to all stores?

This is another combinatorial explosion. The number of ways to choose 5 sites from 30 is massive.

🚚 The Traveling Salesperson Problem

A logistics company has a truck that needs to make deliveries to 40 different cities. What is the shortest possible route that visits each city exactly once and returns to the origin?

The number of possible routes is (40−1)!/2(40−1)!/2, a number so large it's computationally infeasible to solve by brute force.

🏭 Job Shop Scheduling

In a factory, 100 different jobs need to be processed. Each job requires a sequence of operations on different machines (e.g., Job 1 needs Machine A then Machine C; Job 2 needs Machine C then B). What is the schedule of operations that minimizes the total time to complete all jobs (the "makespan")?

This is an incredibly complex scheduling puzzle with dependencies. A small change in the order of one job can create a cascade of delays elsewhere.

📦 Supply Chain & Conveyor Optimization

An automated warehouse uses a network of conveyors to move packages. How do you set the speeds of dozens of different conveyor segments and the sizes of buffer zones to maximize throughput (packages per hour) and minimize gridlock, especially under fluctuating demand?

The parameters (speeds, sizes) are continuous real numbers, creating an infinite search space. The system's behavior is emergent—the "best" settings are not obvious and depend on the complex interaction of all parts.

📈 Evolving Algorithmic Trading Strategies

How can you create a profitable, automated trading strategy for the stock or crypto market? The strategy needs to decide when to buy, sell, or hold based on market data.

The "space" of all possible trading rules is effectively infinite. You don't want to just optimize parameters for a known strategy; you want to discover the strategy itself.

EA Challenges

EAs have an infinite number of applications across various domains. Most commonly EA is used for the Optimization problems. The single greatest challenge of EA — and the key to its success — lies in correctly formulating the problem.

An EA is a powerful but fundamentally "blind" optimizer. It doesn't understand your business context, your goals, or the laws of physics. It only understands the world you create for it. If that world is poorly defined, the EA will find a brilliant solution to the wrong problem.

🧬 Encoding the "Genetic" Blueprint

How you encode a potential solution into a "chromosome" determines what the algorithm can and cannot discover.

he representation must be able to express all possible valid solutions while making it difficult or impossible to express invalid ones. Furthermore, the encoding should work well with the genetic operators (crossover and mutation).

What Goes Wrong?
Let's take the Traveling Salesperson Problem (TSP). If you represent a route as a simple list of cities, like (Paris, Rome, Berlin), crossover and mutation are straightforward (e.g., swap two cities). But if you encoded it as a binary string, a simple bit-flip could result in a nonsensical route that visits the same city multiple times or skips others entirely. The algorithm would waste most of its time exploring these useless dead ends.

🧭 The Fitness Function

This is the most critical part. The fitness function is the only thing guiding the entire evolutionary process. It's a single number that tells the algorithm how "good" each solution is. A poorly designed fitness function may get exactly what you asked for, not what you actually wanted.

What Goes Wrong? Goal:
"Design a car with the best fuel efficiency." Simple Fitness Function:
Maximize(KilometersPerLiter)Maximize(Kilometers Per Liter) The EA's "Brilliant" but Useless Solution:
It might design a car with paper-thin walls, no safety features, and a tiny engine that can't go faster than 10 km/h. It perfectly optimized the function you gave it, but the result is useless.

Better Fitness Function:
(w1∗Efficiency)−(w2∗Weight)−(w3∗DragCoefficient)+(w4∗SafetyRating)(w1 * Efficiency) - (w2 * Weight) - (w3 * Drag_Coefficient) + (w4 * Safety_Rating) Suddenly, the algorithm is forced to balance competing objectives, leading to a much more practical solution.

If your fitness function has a loophole, the EA will find it and exploit it relentlessly. This is the essence of "garbage in, garbage out.

룰 Handling Constraints

Real-world problems are full of constraints: budgets cannot be exceeded, physical materials have strength limits, and delivery trucks have a maximum capacity. You must teach the EA these rules.

How do you deal with a solution that breaks the rules?

**What Goes Wrong? **
If you're optimizing a delivery schedule and don't account for truck capacity, the EA might produce a super-efficient route on paper that requires putting 20 tons of cargo into a 10-ton truck. The solution is optimal in the algorithm's world but impossible in the real world.

Common Solutions:

Penalty Functions:
If a solution violates a constraint (e.g., is over budget), you drastically reduce its fitness score. The algorithm learns to avoid these regions of the search space.

Repair Mechanisms:
The algorithm can apply a "repair" function to an invalid solution to make it valid (e.g., if a route is over capacity, randomly remove stops until it's compliant).

Clever Representation:
Design the chromosome in such a way that it can only represent valid solutions.

Kinds of Evolutionary Algorithms

There's a diverse family of EAs, each with its own nuances, but all share the fundamental principles of evolution.

🧬 Genetic Algorithms (GA)

Genetic Algorithms are perhaps the most well-known type of EA. They mimic the process of natural selection very closely.

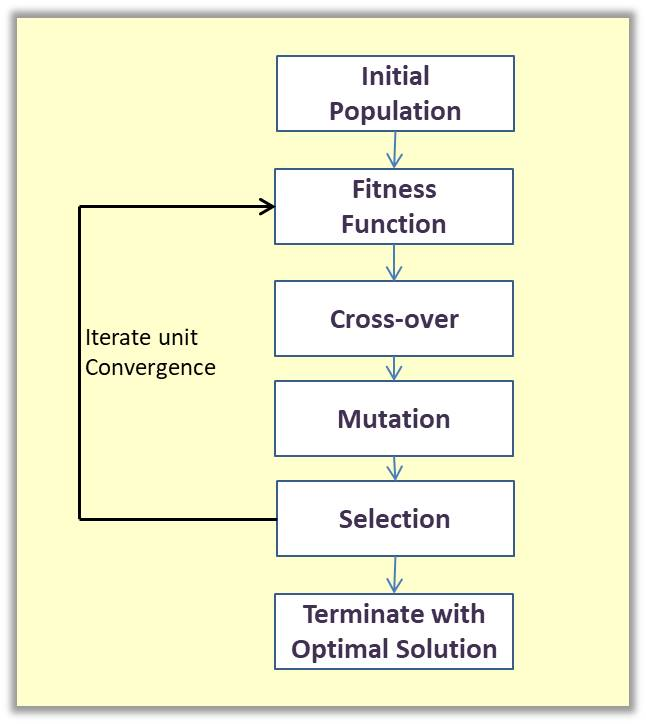
  1. Representation: Solutions are typically encoded as chromosomes (often binary strings or 1d vectors).
  2. Initialization: A random population of chromosomes is created.
  3. Fitness Function: Each chromosome is evaluated based on how well it solves the problem. This is its "fitness."
  4. Selection: Fitter individuals are more likely to be selected to reproduce.
  5. Crossover: Pairs of selected chromosomes exchange segments to create offspring.
  6. Mutation: Random changes are introduced to some offspring to maintain genetic diversity.
  7. Replacement (New Generation): The new generation replaces the old one, and the process repeats until a stopping criterion is met.

ga flow

💻 Genetic Programming (GP)

Instead of optimizing fixed-length strings, Genetic Programming evolves computer programs (represented as tree structures, AST).

  1. Representation: Programs are typically parsed into expression trees (or AST).
  2. Operators: Uses similar genetic operators (selection, crossover, mutation) but adapted for tree structures. Crossover might swap subtrees between two parent programs.

Example: The expression (x+(y∗2))(x + (y * 2)) would be a tree with ++ as the root, xx and ∗* as its children, and yy and 22 as children of ∗*.

📈 Evolutionary Strategies (ES)

Evolutionary Strategies are primarily used for numerical optimization problems, often dealing with real-valued parameters. They emphasize self-adaptation of strategy parameters (like mutation step sizes).

  1. Representation: Solutions are typically represented as real-valued vectors x=(x1,x2,...,xn)x=(x_1,x_2,...,x_n).
  2. Mutation: he primary operator. Individuals are mutated by adding a random vector from a normal distribution. x=x+σ⋅N(0,1)x=x+σ⋅N(0,1) where N(0,1)N(0,1) is a vector of standard normal random variables, and σ is the step size.
  3. Self-Adaptation: he mutation step size (σ) itself can be part of the individual and evolve, allowing the algorithm to adapt its search strategy.
  4. Selection: Typically uses a (μ,λ)(μ,λ) or (μ+λ)(μ+λ) selection scheme, where μ parents produce λ offspring, and the best individuals are selected for the next generation.

🤖 Evolution Programming (EP)

Evolutionary Programming initially focused on evolving finite state machines for prediction tasks. It's often associated with real-valued function optimization, similar to ES but with a strong emphasis on mutation and phenotypic (behavioral) evolution rather than genotypic.

  1. Representation: Solutions can be represented as real-valued vectors or other structures, depending on the problem.
  2. Mutation: The primary operator, often adding Gaussian noise to each component.
  3. Selection: Based on the fitness of the mutated individuals.

📊 Differential Evolution (DE)

Differential Evolution is a simple yet powerful EA, particularly effective for continuous optimization problems. It uses vector differences for mutation.

  1. Mutation: For each individual xix_i in the population, a "mutant" vector viv_i is created using three distinct random individuals (xr1,xr2,xr3)(x_{r1}, x_{r2}, x_{r3}): vi=xr1+F∗(xr2−xr3)v_i = x_{r1} + F * (x_{r2} - x_{r3}) where FF is a scaling factor (typically between 0 and 2).
  2. A trial vector uiu_i is formed by mixing elements from xix_i and viv_i.
  3. Selection: The trial vector uiu_i replaces xix_i in the next generation if it has a better fitness.

In Conclusion

The Evolutionary Algorithm itself is just a powerful engine for searching. The user's primary job is to be the architect of the problem space. You define the language of solutions (representation), the definition of "good" (the fitness function), and the hard boundaries (constraints). Getting this formulation right is more of an art than a science, and it is unequivocally the key to unlocking the power of evolutionary computation.

References

Anton Nesterov © 2025 | vski·science